
قیمت 19,000 تومان
منحنی های شکنندگی
منحنی های شکنندگی …………………………………………………………………………………………….
2-1 منحنی های شکنندگی لرزهاي……………………………………………………………………………………………..
2-1-1 منحنی های شکنندگی تجربی………………………………………………………………………………………..
2-1-2 منحنی های شکنندگی بر اساس قضاوت مهندسی……………………………………………………………..
2-1-3 منحنی شکنندگی تحلیلی………………………………………………………………………………………..
2-1-4 منحنی شکنندگی ترکیبی……………………………………………………………………………………………….
2-2 توابع شکنندگی………………………………………………………………………………………………………………..
2-3 حالات خرابی در دستورالعمل HAZUS…………………………………………………………………………..
2-4 دستورالعمل HAZUS……………………………………………………………………………………………………
2-4-1 طبقهبندی ساختمانها در HAZUS……………………………………………………………………………..
2-4-2 منحنی شکست در HAZUS………………………………………………………………………………………
2-5 پیشینهی تحقیق………………………………………………………………………………………………………………..
2-5-1 پژوهش جوزف کارلو مارانو و همکاران…………………………………………………………………………
2-5-2 مطالعات روییزگارسیا و همکاران…………………………………………………………………………………..
2-5-3 مطالعات شکنندگی در تایوان برای زلزلهی چیچی………………………………………………………….
2-5-4 مطالعات میشاییل تانتالا و جورج دوداتیس………………………………………………………………………
2-5-5 مطالعات اربریک و الناشی…………………………………………………………………………………………..
2-5-6 سایر مطالعات……………………………………………………………………………………………………………..
منابع
منحنی های شکنندگی لرزهای
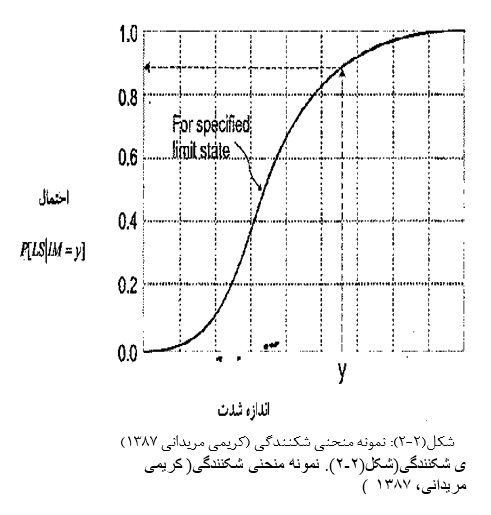
منحنی های شکنندگی، احتمال خرابی متناظر با یک حالت خرابی معین را در چندین سطح از جنبش هاي لرزه اي زمین بیان میکند. در واقع منحنی شکنندگی، نسبت بین شدت زمین لرزه و سطح خرابی لرزه اي محتمل را توصیف میکند. جهت تعیین دقیق چنین نسبتی انتخاب صحیح شدت زلزله در منطقه ی سازهي تحت بررسی مهم میباشد. از شاخص هایی که شدت زلزله را بطور مناسب جهت تحلیل شکنندگی معرفی مینمایند میتوان از بیشینه شتاب زمین PGA، بیشینه سرعت زمین PGV، بیشینه تغییر مکان زمین PGDنام برد. این منحنی ها را میتوان از تحلیل رگرسیون منطقی اطلاعات خرابی واقعی یا شبیه سازي شده و یا روشهاي حل عددي بدست آورد.
با توجه به اینکه آسیب پذیری لرزه ای زمانی رخ میدهد که احتمال فراگذشت سازه از سطح خرابی تعریف شده وجود داشته باشد، گسیختگی زمانی رخ میدهد که سازهی موجود نتواند شرایط لازم برای سطح عملکرد تعریف شده را ارضا کند.
استفاده از منحنی شکست برای ارزیابی رفتار سازه ها و خطر ناشی از زلزله، در دو دهه ی اخیر به طور گسترده ای توسط جامعهی علمی مورد استفاده قرار گرفته است. روش منحنی شکست یک امتیاز مهم دارد و آن امتیاز، این است که آسیب پذیری سازه و مؤلفههای آن را با یک روش ساده نشان میدهد و اجازه میدهد که سطح خرابی مورد انتظار برای شدت زلزلهی معین را تخمین بزنیم ( مارانو ،2009)[1].
روش های مختلفی برای تهیهی منحنی شکست وجود دارد که مهم ترین آنها به شرح زیر است:
- روش تجربی[2] یا آزمایشگاهی
- روش قضاوت مهندسی[3]
- روش تحلیلی[4]
- روش ترکیبی [5]که توضیحات مربوط به هر روش در ادامه آمده است.
منحنی های شکنندگی تجربی
منحنی های شکنندگی بر اساس مشاهدات اطلاعات مربوط به آسیب های سازه ای به دست آمده از زلزله های گذشته به دست میآید. این منحنیها انواع مختلف سازه را مشخص نمی کنند. یعنی تأثیر پارامتر های مکانیکی ساختمان، عملکرد ساختمان ( استاتیکی یا دینامیکی )، تغییرات ورودی (حوزه ی فرکانسی ) و … در نظر گرفته نمی شود. بنابراین این روش برای تعیین سطح خرابی یک سیستم خاص مناسب نمیباشد.
منحنی های شکنندگی تجربی، اغلب همراه با کمبود داده میباشند و فقط قابل استفاده در مناطق محدود هستند ولی از آنجایی که منحنی های شکنندگی تجربی برگرفته از مشاهدات خسارت هاي ناشی از زلزلههاي واقعی روي سازه هستند، نقش اجتناب ناپذیري در مطالعه روي منحنی هاي شکنندگی ایفا میکنند. منحنی هاي شکنندگی تجربی در صورت تعیین براساس داده هاي خرابی به تعداد کافی میتوانند به عنوان معیار در برآورد صحت منحنی های شکنندگی تحلیلی و آن دسته از منحنی هاي آزمایشگاهی که فقط تحت شرایط آزمایشگاهی ایجاد میشوند، مورد استفاده قرار داده شوند ( نیلسن، 2005 ).
منحنی های شکنندگی تجربی دارای محدودیت های زیر میباشند:
- محدودیت اول این است که دست یابی به تعداد کافی از یک سازهی خاص که در یک سطح خرابی قرار میگیرند، بسیار سخت و حتی غیر ممکن است. این محدودیت، موردي است که رسیدن به نتایج آماري دقیق را مشکل میکند( شینوزوکا ، 1998 ). از این رو باید تعداد کافی از سازه هایی که تحت یک حالت خرابی واقع میشوند در دسترس باشند. بنابراین اعتبار این نوع منحنی هاي شکنندگی کاهش مییابد.
- محدودیت دوم وابستگی نتایج به ثبت شدت هاي زمین لرزه میباشد ( باسوز و کیرمدجان، 1999 )
- محدودیت سوم، مغایرت نظرات بازرسین در اختصاص سطوح خرابی است ( باسوز و کیرمدجان، 1999 ).
از این رو عدم قطعیت هاي زیادي در منحنی های شکنندگی تجربی وجود دارد و استفاده از این روش در مناطقی که تجربهی تعداد زلزلههای کافی را نداشته باشند قابل قبول نیست.
منحنی های شکنندگی بر اساس قضاوت مهندسی
این منحنی ها بر اساس قضاوت و تجربه ی متخصصین مربوطه، در مورد سازهی مورد مطالعه تهیه می شوند و عدم قطعیت زیادی دارند. یکی از مهم ترین عدم قطعیت ها ناشی از قضاوت مهندسی است که به تجربیات و تعداد متخصصین وابسته است و دیگری به تعداد تیپ های سازه های مورد بررسی بستگی دارد. این عدم قطعیت ها تأثیر زیادی در پاسخ ها دارند، اما امکان کمی کردن آنها وجود ندارد ( نیلسن، 2005 ).
منحنی های شکنندگی تحلیلی
هنگامی که اطلاعات خرابی واقعی کافی دربارهی مدل مورد مطالعه و داده های زمینلرزه در دسترس نباشند، منحنی های شکنندگی تحلیلی جهت ارزیابی عملکرد سازه ها مورد استفاده قرار میگیرند ( نیلسن، 2005).
منحنی شکست تحلیلی با استفاده از شبیه سازی عددی یا تحلیل تصادفی سازه های قرار گرفته در معرض رکورد های مصنوعی به دست میآید. با این روش میتوان آسیب پذیری انواع مختلف سازه ها را بدون داشتن تجربهی زمین لرزهی زیاد ارزیابی کرد ( یامازاکی، 2003).
طبقه بندی ساختمان ها در HAZUS
تقسیم بندی کلی سازهها از نظر کاربری در دستورالعمل HAZUS شامل سازههای مسکونی، تجاری، صنعتی، کشاورزی، مذهبی، دولتی و آموزشی و… میباشد. علاوه براین انواع سازهها از لحاظ سیستم ساختمانی نیز طبقهبندی شدهاند. اطلاعات مورد نیاز برای تحلیل و ارزیابی احتمال وقوع خرابی در اثر زلزله با طبقهبندی و نوع سازهها ارتباط دارد. در واقع هدف اصلی از تقسیمبندی انواع مختلف سازهها این است که ساختمانهایی که ویژگیهای مشابهی دارند و احتمالاً در اثر زلزله نیز دچار خرابی مشابهی میشوند در یک طبقه قرار بگیرند.
در تقسیم بندی سازهها، ارتفاع آنها نیز در نظر گرفته شده است تا از این طریق تفاوت پریود سازهها و سایر پارامترهای طراحی که با ارتفاع سازه مرتبط هستند، در ارزیابی خطرات لرزهای در نظر گرفته شود.
علاوه بر این موارد تقسیم بندیهای دیگری نیز برای سیستم حمل و نقل شامل سیستمهای بزرگراهی، راهآهن، سیستم حمل و نقل اتوبوس، فرودگاه و بندرگاه درنظر گرفته شده است.
دستورالعمل HAZUS انواع سازهها را از لحاظ روش طراحی به 4 گروه طبقه بندی کرده است که شامل موارد زیر میباشد:
- حالت طراحی High- code طبق استانداردهای طراحی لرزهای.
- حالت طراحی Moderate-code طبق استانداردهای طراحی لرزهای.
- حالت طراحی Low-code طبق استانداردهای طراحی لرزهای.
- حالت طراحی Pre-code که شامل ساختمانهایی است که طبق ضوابط لرزهای طراحی نشدهاند.
منحنی شکست در HAZUS
یکی از روشهایی که برای ارزیابی آسیبپذیری لرزهای در HAZUS مورد استفاده قرار گرفته است، استفاده از منحنی های شکنندگی میباشد. در منحنی شکنندگی، احتمال وقوع هریک از حالات خرابی معرفی شده در مقابل مقادیر مختلف PGA مورد بررسی قرار میگیرد.
اطلاعات مورد نیاز برای تخمین خرابی سازهها با استفاده از منحنی های شکنندگی به شرح زیر میباشد:
- نوع سیستم ساختمانی، ارتفاع ساختمان و نوع طراحی لرزهای.
- طیف پاسخ یا مقدار PGA در منطقهای که ساختمان در آن واقع شده است.
نهایتاً،منحنی های شکنندگی احتمال رسیدن یا فراگذشت سازه را از هریک از حالتهای خرابی را در مقادیر مختلف PGA نمایش میدهد از این منحنیها میتوان برای تخمین خسارات فیزیکی، مالی و اجتماعی استفاده کرد. شکل 2-4 یک نمونه منحنی شکست بر حسب جابجایی طیفی در مقابل احتمال رسیدن یا فراگذشت از 4 حالت خرابی را ارائه میدهد.
جهت مشاهده نمونه های دیگر از ادبیات ، پیشینه تحقیق و مبانی نظری پایان نامه های مهندسی عمران کلیک کنید.
نمونه ای از منابع لاتین منحنی های شکنندگی
- Algan, B., 1982. Drift and Damage Considerations in Earthquake-Resistant Design of Reinforced Concrete Buildings, PhD thesis, Department of Civil Engineering, University of Illinois at Urbana Champaign.
- Altug Erberik, M., Amr S. Elnashai, 2004. Fragility analy sis of flat-slab structures. Journal of Engineering Structures ,pp. 937-948.
- Bakhshi & karimi.1385.Method of developing Fragility Curve a case Study for seismic Assement of Masonry Building in IRAN.
- Banon, H., Biggs, J. M., Irvine, M., 1981. Seismic Damage in Reinforced Concrete Frames. ASCE, Journal of Structural Engineering, Vol. 107, No. ST9, pp.1713-1729.
- Basoz , and Kiremidjian, Anne, S., 1996. Risk Assessment for Highway Transportation Systems. Report No.NCEER-118, John A. Blume Earthquake Engineering Center.
- Basoz, , Kiremidjian , A., king, S.A., and law , K.H., 1999. Statistical analysis of bridge damage data from the 1994 Northridge , CA , Earthquake , earthquake spectra,vol.15,no.1.
- Bouc R. Forced vibration of mechanical systems with hysteresis. In: Proceedings of the 4th conf. on nonlinear oscillation. 1967.
- Y and V. Bertero. 2001. Improved shaking and damage parameters for post-earthquake applications. SMIP01 seminar Proceedings.
- Clough RW, Penzien J. Dynamics of structures. New York: McGraw-Hill, Inc.;1977.
- Deodatis, G., Shinozuka, M., Saxena, , 2000. Effect of spatial variability of Ground motion on bridge fragility curves. , 8th ASCE Specialty conference on probabilistic Mechanics and structural reliability.
- Porter.M. 2003. The Economic Performance of Regions. Carfax Publishing.
- Earthquake loss estimation Hazus – MH MR5. Technical & User’s Manual.
- FEDERAL EMERGENCY MANAGEMENT AGENCY.2000. FEMA 356.
- ….
- ….
نقد و بررسیها
هنوز بررسیای ثبت نشده است.









نقد و بررسیها
هنوز بررسیای ثبت نشده است.